Det er ofte svært at vurdere, om man skal melde videre, når modstanderne har konkurreret på 5‑trinet. Det har ført til det velkendte mundheld “5‑trinet tilhører modparten”.
Overskriftens omskrivning heraf refererer til, at turneringslederen måtte i aktion, da Nord havde tænkt sig om i længere tid, hvilket efter Ø-V’s mening havde hjulpet Syd til at gå imod mundheldet og melde videre.
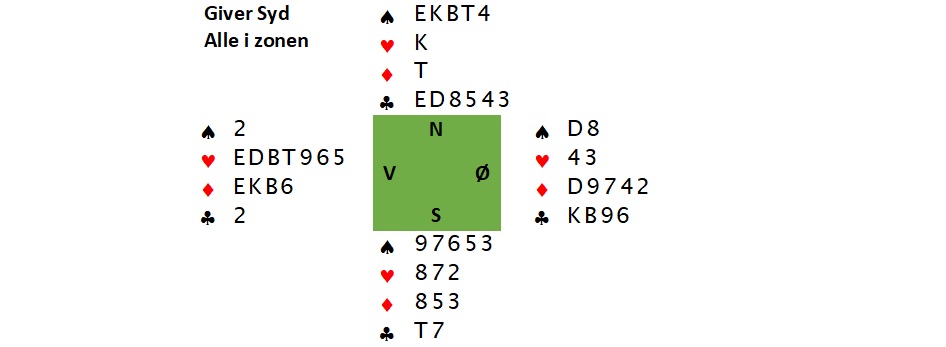

Spillet stammer fra en butlerturnering, hvor taktikken er som i holdkamp.
Syd havde ikke mange værdier til sin 4♠‑melding, men på den anden side var der heller ingen spildte værdier i Nords kortfarver!
Vest konkurrerede i 5♥, og Nord havde et problem – skal man melde videre, eller skal man tage pengene i 5♥, hvis der ellers er nogen penge at hente? Efter et minuts tænkepause valgte Nord at doble.
Syds modspilsværdier var til at overskue, og han valgte derfor at tage ud i 5♠. Vest doblede, men inden han spillede ud, tilkaldte han turneringslederen for at gøre opmærksom på, at tænkepausen kunne have haft indflydelse på Syds melding (i Danmark er det normalt tilstrækkeligt at enes med modstanderne om, at der har været en tænkepause, og først tilkalde turneringslederen efter spillet, hvis det stadig er relevant).
Kontrakten gik to doblede beter, da Nord blev mattet, inden klørfarven blev rejst. Men Vest konstaterede, at 5♥ var bet med ♥K ude af plads, og derfor gjorde han ikke mere ved sagen.
Skal turneringslederen justere scoren?
Spillerne diskuterede efterfølgende, om scoren skulle have været justeret, hvis 5♥‑D havde vundet. Med andre ord – er Syds 5♠‑melding lovlig?
Som sædvanlig skal vi stille to spørgsmål, når der er ubeføjede oplysninger:
- Er pas et logisk alternativ for Syd?
- Gør pausen det attraktivt at melde 5♠ i stedet?
Efter min vurdering er svaret “ja” til begge spørgsmål. Syd har ganske vist ingen hjælp i modspillet, men hans hånd vil også være en skuffelse for makker i en 5♠‑kontrakt. Hvis makker har tilstrækkelig offensiv til, at det er bedre at spille 5♠ end at vælge modspil i 5♥‑D, kunne makker meget vel have meldt det selv. Pas må være en mulighed, der vil blive valgt af tilstrækkelig mange spillere til, at det udgør et logisk alternativ.
Nords lange tænkepause tyder på, at han enten er usikker på, om 5♥ overhovedet kan sættes, eller at han har ekstra fordeling og overvejer at melde 5♠ selv. Uanset hvilken af disse muligheder der er tale om, er det blevet attraktivt for Syd at melde 5♠.
Derfor skal turneringslederen justere scoren, hvis Ø-V er skadet af, at Syd meldte 5♠ i stedet for pas.
Spilføringsproblemet
Vests konstatering af, at han har 3 tabere i 5♥, var noget overfladisk, for spillet har flere interessante tekniske pointer. Se engang på Vests spilføringsproblem. Hvis Nord starter med to høje spar mod 5♥‑D, må Vest trumfe. Der er kun én indkomst til bordet, så man kan ikke fange ♥Kxx i plads. Da Nord forventes at være kort i hjerter, kan Vest meget vel vælge at trække ♥E fra hånden i stedet, og så har han pludselig 12 stik!
Hvis Vest vil spille på hjerterknibningen, kan han vælge at stikke ♦B over på bordet. Når Nord har ru10 blank, har Vest en ekstra indkomst på bordet. Derved kan Vest knibe Syd for ♥Kxx i dette ene tilfælde (tak til nogle kvikke læsere for at gøre opmærksom på denne mulighed).
Nord bør imidlertid trække ♠K i udspillet. Med ♠D på bordet er der ingen tvivl om, at Syd vil længdemarkere i stik 1, og så vil Nord måske skifte til ♣E og mere klør i håb om, at Syd kan trumfe.
Spiller Nord på denne måde, har Vest de nødvendige indkomster til at knibe Syd for ♥Kxx. Men måske bliver Vest mistænksom over denne græske gave og topper alligevel ♥K ud! Det er vanskeligt at vurdere sandsynlighederne, men hvis vi er lidt flinke over for Vest, som jo er ikke‐fejlende, er følgende måske fornuftigt:
- 1/3 for 5♥‑D 10 stik = +200
- 1/2 for 5♥‑D 11 stik = −850
- 1/6 for 5♥‑D 12 stik = −1050
Det aktuelle resultat ved bordet var −500, så det er ikke let at overskue, om Ø-V er skadet. Det ser vi på i næste afsnit. Da det kan være lidt tung læsning, vil jeg straks ødelægge spændingen og afsløre, at Ø-V ikke er skadet (men det er tæt på).
For regnskabsnørderne
Medmindre du er interesseret i de tekniske detaljer om, hvordan man beregner vægtede scorer i en butlerturnering, kan du roligt stå af her! Videre læsning er således på eget ansvar – jeg vil ikke høre klager om, at dette er for nørdet.
De fleste regnskabsprogrammer, herunder BridgeCentral, kan beregne den vægtede score automatisk, men jeg gennemgår alligevel metoden her.
Først og fremmest må du endelig ikke gange brøkerne direkte på scorerne +200, −850 og −1050. I stedet beregnes hypotetisk det resultat i imp eller parpoint, afhængigt af regnskabsformen, som hvert af de tre scorer ville føre til, hvorefter brøkerne ganges på disse resultater.
Lad os se, hvordan det fungerer i en butlerturnering. Aktuelt bestod turneringen af 9 borde, og resultaterne var følgende, idet resultatet ved vores bord er markeret med en stjerne:
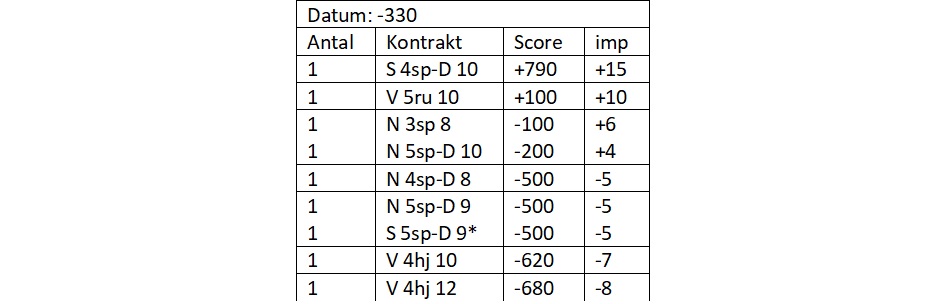
Spillets datumscore beregnes som gennemsnittet af samtlige scorer undtagen den yderste i hver ende, afrundet til nærmeste tier, og i dette tilfælde giver det −330 (altså 330 til Ø-V).
Ved vores bord var resultatet −500, dvs. Ø-V vandt 5 imp på spillet for en forskel på 170 i forskel til datumscoren.
Når vi erstatter resultatet med den vægtede score, bliver billedet lidt mere kompliceret. Af hensyn til de videre beregninger har jeg delt scoren for V 4♥ 12 op i to bidder.
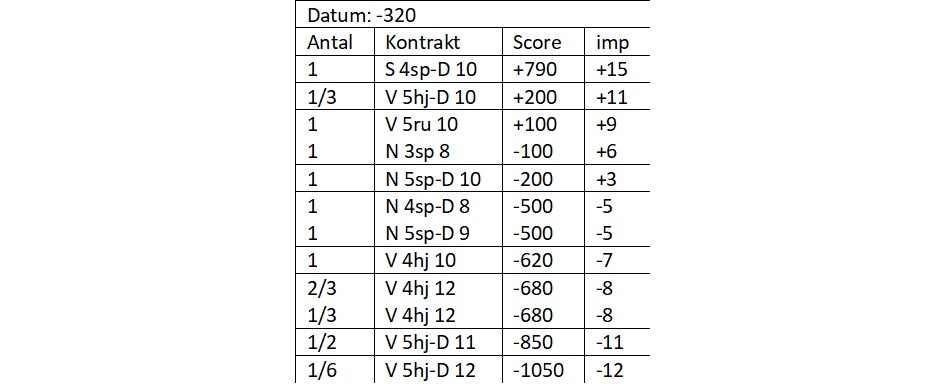
Den yderste score i Ø-V’s favør består nu af 1/6 af 5♥-D 12, 1/2 af 5♥-D 11, og 1/3 af 4♥ 12! Når vi tager disse bort sammen med 4♠‑D 10 i den anden ende, bliver gennemsnittet −320 efter afrunding.
Nu kan vi beregne resultatet ved vores bord for N-S:
- 1/3 af 11 imp (svarende til +200 mod −320)
- 1/2 af −11 imp (svarende til −850 mod −320)
- 1/6 af −12 imp (svarende til −1050 mod −320)
Lægger vi disse tal sammen, bliver scoren −3,83 imp, dvs. Ø-V vinder 3,83 imp, når vi beregner den vægtede score. Men ved bordet vandt Ø-V 5 imp, og det betyder, at Ø-V faktisk tjente 1,17 imp på Syds 5♠‑melding. Derfor skal vi ikke justere scoren. Resultatet i 5♠‑D står således ved magt.